-

Some New Results About Trigonometry in Finite Fields
Habib Hosseini,
Naser Amiri
Issue:
Volume 5, Issue 4, August 2016
Pages:
93-96
Received:
23 April 2016
Accepted:
21 May 2016
Published:
17 June 2016
Abstract: In this paper we study about trigonometry in finite field, we know that 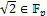 , the field with p elements, where p is a prime number if and only if p = 8k + 1 or p = 8k + 1 or p = 8k + 1 or p = 8k−1. Let F and K are two field, we say that F is an extension of K, if K ⊆ F or there exist a monomorphism f: K → F. recall that
, the field with p elements, where p is a prime number if and only if p = 8k + 1 or p = 8k + 1 or p = 8k + 1 or p = 8k−1. Let F and K are two field, we say that F is an extension of K, if K ⊆ F or there exist a monomorphism f: K → F. recall that 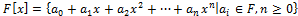 , F[x] is the ring of polynomial over F. If K
, F[x] is the ring of polynomial over F. If K 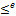 F (means that F is an extension of K) an element u εF is algebraic over K if there exists f(x) ε K[x] such that f(u)=0. The algebraic closure of K in F is
F (means that F is an extension of K) an element u εF is algebraic over K if there exists f(x) ε K[x] such that f(u)=0. The algebraic closure of K in F is 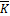 , is the set of all algebraic elements in F over K.
Abstract: In this paper we study about trigonometry in finite field, we know that
, is the set of all algebraic elements in F over K.
Abstract: In this paper we study about trigonometry in finite field, we know that 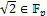 , the field with p elements, where p is a prime number if and only if p = 8k + 1 or p = 8k + 1 or p = 8k + 1 or p = 8k−1. Let F and K are two field, we say that F is an extension of K, if K ⊆ F or there exist a monomorphism f: K → F. recall that
, the field with p elements, where p is a prime number if and only if p = 8k + 1 or p = 8k + 1 or p = 8k + 1 or p = 8k−1. Let F and K are two field, we say that F is an extension of K, if K ⊆ F or there exist a monomorphism f: K → F. recall that 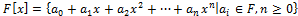 , F[x] is the ring o...
Show More
, F[x] is the ring o...
Show More
-

Reduction of Mortality Rate Due to AIDS When Treatment Is Considered
Issue:
Volume 5, Issue 4, August 2016
Pages:
97-102
Received:
16 May 2016
Accepted:
28 May 2016
Published:
18 June 2016
Abstract: AIDS is one of the most threatening diseases for human being that is caused by a virus named HIV. Here the reduction of the death rate after infected by AIDS has been discussed. A mathematical model of HIV has been formulated. Then its positivity and boundedness has been investigated. It has been shown that it is possible to minimize the mortality rate by providing the treatment to the HIV infected people. Moreover, the control of the transfer rate from the infected class to the AIDS class reduces the disease rate. The increasing of the transfer rate from the infected class to the treated class also reduces the mortality rate.
Abstract: AIDS is one of the most threatening diseases for human being that is caused by a virus named HIV. Here the reduction of the death rate after infected by AIDS has been discussed. A mathematical model of HIV has been formulated. Then its positivity and boundedness has been investigated. It has been shown that it is possible to minimize the mortality ...
Show More
-

The 3-Block KSOR Method for Full Rank Rectangular Systems
I. K. Youssef,
Salwa M. Ali,
M. A. Naser
Issue:
Volume 5, Issue 4, August 2016
Pages:
103-107
Received:
24 May 2016
Accepted:
2 June 2016
Published:
21 June 2016
Abstract: A new version of the KSOR method is considered to introduce the least squares solution of a full rank over determinant system of linear algebraic equations. The treatment depends on introducing an augmented non-singular square system through splitting the coefficient matrix A into two matrices A1, A2 with non-singular part, A1. Accordingly, a new version of the 3-block SOR method is introduced, the 3-block KSOR method. Selection of the relaxation parameter which guarantees the convergence in the sense of reducing the spectral radius of the iteration matrix is considered. Application of the theoretical results to a numerical example has confirmed the expected behaviour of the 3-block KSOR method.
Abstract: A new version of the KSOR method is considered to introduce the least squares solution of a full rank over determinant system of linear algebraic equations. The treatment depends on introducing an augmented non-singular square system through splitting the coefficient matrix A into two matrices A1, A2 with non-singular part, A1. Accordingly, a new v...
Show More
-

The Problem of Countability of Highest Ordinals
Alexey Pavlovich Kulaichev
Issue:
Volume 5, Issue 4, August 2016
Pages:
108-112
Received:
16 March 2016
Accepted:
25 March 2016
Published:
28 June 2016
Abstract: In this study we use the alternate point of view on the structure of ordinals, according to which each ordinal is the union of non-intersecting foregoing segments of ordinals of equal exponentiation. Each ordinal 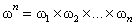 is seen as the union
is seen as the union 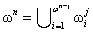 for any j=1, n-1 instead traditional union of foregoing intersecting segments of ordinals of consistently increasing exponentiation
for any j=1, n-1 instead traditional union of foregoing intersecting segments of ordinals of consistently increasing exponentiation 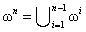 . The first form corresponds to the geometric representation of ordinal
. The first form corresponds to the geometric representation of ordinal 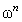 as an infinite n-dimensional matrix. According traditional formulation
as an infinite n-dimensional matrix. According traditional formulation 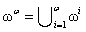 , thus
, thus 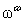 is
is 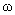 -countable union of countable ordinals so
-countable union of countable ordinals so 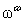 is countable. According to alternate formulation
is countable. According to alternate formulation 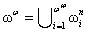 for any n, thus
for any n, thus 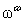 is
is 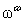 -union of ordinals and the findings will be different. These findings are: 1) the proof of countability of countable union of countable ordinals can not be directly or inductively transferred to its first limit
-union of ordinals and the findings will be different. These findings are: 1) the proof of countability of countable union of countable ordinals can not be directly or inductively transferred to its first limit 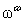 -union; 2)
-union; 2) 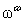 seems to be the first uncountable ordinal with its power is equal to continuum; 3) the subsequent ascending degrees of
seems to be the first uncountable ordinal with its power is equal to continuum; 3) the subsequent ascending degrees of 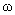 -exponentiation of
-exponentiation of 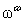 , i.e.
, i.e. 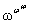 ,
, 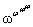 ,..., correspond to consecutive
,..., correspond to consecutive 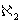 ,
, 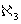 ,
, 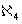 , ... cardinals; 4) from here it also follows the direct justification of continuum hypothesis. Our study shows that in the domain of transfinite sets different points of view and its findings have the legal right to coexist as Nels Bohr's principle of complementarity in physics.
Abstract: In this study we use the alternate point of view on the structure of ordinals, according to which each ordinal is the union of non-intersecting foregoing segments of ordinals of equal exponentiation. Each ordinal
, ... cardinals; 4) from here it also follows the direct justification of continuum hypothesis. Our study shows that in the domain of transfinite sets different points of view and its findings have the legal right to coexist as Nels Bohr's principle of complementarity in physics.
Abstract: In this study we use the alternate point of view on the structure of ordinals, according to which each ordinal is the union of non-intersecting foregoing segments of ordinals of equal exponentiation. Each ordinal 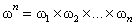 is seen as the union
is seen as the union 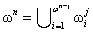 for any j=1, n-1 instead traditional union of foregoing intersecting segments of ordinals of consistently increasi...
Show More
for any j=1, n-1 instead traditional union of foregoing intersecting segments of ordinals of consistently increasi...
Show More
-

The QR Method for Determining All Eigenvalues of Real Square Matrices
Issue:
Volume 5, Issue 4, August 2016
Pages:
113-119
Received:
23 November 2015
Accepted:
3 December 2015
Published:
23 July 2016
Abstract: Eigenvalues are special sets of scalars associated with a given matrix. In other words for a given matrix A, if there exist a non-zero vector V such that, AV= λV for some scalar λ, then λ is called the eigenvalue of matrix A with corresponding eigenvector V. The set of all nxm matrices over a field F is denoted by Mnm (F). If m = n, then the matrices are square, and which is denoted by Mn (F). We omit the field F = C and in this case we simply write Mnm or Mn as appropriate. Each square matrix AϵMnm has a value in R associated with it and it is called its determinant which is use full for solving a system of linear equation and it is denoted by det (A). Consider a square matrix AϵMn with eigenvalues λ, and then by definition the eigenvectors of A satisfy the equation, AV = λV, where v={v1, v2, v3…………vn}. That is, AV=λV is equivalent to the homogeneous system of linear equation (A-λI) v=0. This homogeneous system can be written compactly as (A-λI) V = 0 and from Cramer’s rule, we know that a linear system of equation has a non-trivial solution if and only if its determinant is zero, so the solution λ is given by det (A-λI) =0. This is called the characteristic equation of matrix A and the left hand side of the characteristic equation is the characteristic polynomial whose roots are equals to λ.
Abstract: Eigenvalues are special sets of scalars associated with a given matrix. In other words for a given matrix A, if there exist a non-zero vector V such that, AV= λV for some scalar λ, then λ is called the eigenvalue of matrix A with corresponding eigenvector V. The set of all nxm matrices over a field F is denoted by Mnm (F). If m...
Show More
-

Numerical Solutions of Elliptic Partial Differential Equations by Using Finite Volume Method
Issue:
Volume 5, Issue 4, August 2016
Pages:
120-129
Received:
23 October 2015
Accepted:
16 November 2015
Published:
23 July 2016
Abstract: Solution of Partial Differential Equations (PDEs) in some region R of the space of independent variables is a function, which has all the derivatives that appear on the equation, and satisfies the equation everywhere in the region R. Some linear and most nonlinear differential equations are virtually impossible to solve using exact solutions, so it is often possible to find numerical or approximate solutions for such type of problems. Therefore, numerical methods are used to approximate the solution of such type of partial differential equation to the exact solution of partial differential equation. The finite-volume method is a method for representing and evaluating partial differential equations in the form of algebraic equations [LeVeque, 2002; Toro, 1999]. In the finite volume method, volume integrals in a partial differential equation that contain a divergence term are converted to surface integrals, using the divergence theorem. These terms are then evaluated as fluxes at the surfaces of each finite volume. Because the flux entering a given volume is identical to that leaving the adjacent volume, these methods are conservative. Another advantage of the finite volume method is that it is easily formulated to allow for unstructured meshes. The method is used in many computational fluid dynamics packages.
Abstract: Solution of Partial Differential Equations (PDEs) in some region R of the space of independent variables is a function, which has all the derivatives that appear on the equation, and satisfies the equation everywhere in the region R. Some linear and most nonlinear differential equations are virtually impossible to solve using exact solutions, so it...
Show More
-

Memory Effects in Diffusion Like Equation Via Haar Wavelets
I. K. Youssef,
A. R. A. Ali
Issue:
Volume 5, Issue 4, August 2016
Pages:
130-140
Received:
17 July 2016
Accepted:
26 July 2016
Published:
10 August 2016
Abstract: The memory and hereditary effects of fractional derivatives as well as integral terms are considered in a diffusion like problem. The Haar wavelet operational matrix technique is employed to solve fractional order diffusion equation with time dependent integral term and time dependent boundary condition. The fractional derivative is described in the Caputo sense. The effect of using inverse fractional operator which combines the memory behaviors of the fractional derivatives to all other terms in the equation is disscused. Different Haar bases functions are used (8, 16, 32, 64) and comparison of the wavelet operational matrix is considered. Error analysis is considered. A general numerical example with four subproblems is considered, graphical representation of the different solutions as well as their errors are given.
Abstract: The memory and hereditary effects of fractional derivatives as well as integral terms are considered in a diffusion like problem. The Haar wavelet operational matrix technique is employed to solve fractional order diffusion equation with time dependent integral term and time dependent boundary condition. The fractional derivative is described in th...
Show More
-

Common Fixed Point Theorem in Fuzzy Metric Spaces Under E. A. Like Property
Madhu Shrivastava,
K. Qureshi,
A. D. Singh
Issue:
Volume 5, Issue 4, August 2016
Pages:
141-144
Received:
4 July 2016
Accepted:
25 July 2016
Published:
21 August 2016
Abstract: George and Veeramani [1] modify the concept of fuzzy metric spaces introduced by Kramosil and Michalek [4], Aamri and Moutawakil [8] generalized the notion of non-compatible mapping in metric space by E.A. property.Continuing the above conceptwe prove some commonfixed point theorem for a pair of weakly compatible maps under E.A. Like property.







