Abstract
Cavities separated by multiple vertical partitions and filled with a porous medium present a remarkable thermal insulation quality, offering potential solutions in various engineering fields. The aim of this study is to analyze the impact of the presence of a porous medium on heat transfer through a partitioned cavity. We have developed a numerical model based on the Navier-Stokes and heat transfer equations, solved using Ansys Fluent software. We examine the evolution of the Nusselt number (convection and radiation) as a function of the position of the porous medium inside the cavity, as well as physical properties such as emissivity, wall conductivity and Rayleigh number. Current lines and isotherms are obtained from this numerical model. Nusselt numbers for both convection and radiation are calculated, taking into account the position of the porous medium in the system, as well as the effect of varying physical parameters on heat transfer. It has been observed that the presence of the porous medium leads to a reduction in the rate of heat transfer within the cavity. The further the porous medium is from the hot wall, the more pronounced this reduction. In addition, radiative transfer has a downward influence on convective transfer. Furthermore, the convective transfer rate decreases with increasing emissivity. As far as conductivity is concerned, transfer rates (convective and radiative) initially increase until a maximum Nusselt number is reached, after which they gradually decrease with a further increase in conductivity. Nusselt numbers (convection and radiation) increase as the Rayleigh number increases.
Keywords
Ansys Fluent, Convective, Porous, Transfer, Nusselt
1. Introduction
In recent years, there has been a plethora of results from studies of natural convection in a closed cavity associated with a porous medium. The interest in these studies is linked to numerous engineering applications such as energy storage, thermal insulation, etc.....
There are three modes of heat transfer in a porous medium. One is conduction in the solid under the effect of the thermal gradient, the other is convection in the fluid and finally thermal radiation which exists between solid bodies.
The literature shows that a great deal of work has been done in this field.
For example, Nield and Bejan
, Grosan et al
, and Ouarhlent and Soudani
carried out convection studies in a partially porous filled medium. Ordonez Miranda and Alvarado
| [4] | J. Ordonez-Miranda, J. J. Alvarado-Gil Effect of pore shape on thermal conductivity of porous media) Journal of Materials Science volume 47, pages6733-6740 (2012). https://doi.org/10.1007/s10853-012-6616-7 |
[4]
studied the shape of pores on the thermal conductivity of a porous medium. They showed that when the Rayleigh increases, this generates a high temperature in the pore space, as well as a drop in velocity and pressure in a porous channel.
Dhifaoui et al
| [5] | Belgacem Dhifaoui, Walid Foudhil, Sadok Ben Jabrallah, Ali Belghith. Study behavior of a porous medium traversed by an air flow and subjected to parietal heating. soumis `a chauffage parietal. Jean Jacques BEZIAN. JITH2007, Aug2007, Albis, France. hal-00161178, version 1 (29-08-2007). |
[5]
experimentally studied heat transfer between the heated wall of a vertical channel and the fluid (air) flowing through it. They compared the case of a channel filled only with air with that of a channel containing a porous medium. They concluded that the porous medium intensifies heat transfer, enabling such a system to be used as a heat exchanger.
Alkam et al
demonstrated the effects of porous layer thickness, Darcy number, thermal conductivity ratio and microscopic inertia coefficient on the thermal performance of a rectangular channel containing a porous medium. The results show that the effect of the microscopic inertia coefficient can be neglected if the Darcy number is less than 10
-4. On the other hand, for a high microscopic inertial coefficient, the effect of the Darcy number is negligible. To improve heat transfer, we use inertias with high thermal conductivity, lower Darcy numbers and higher microscopic inertia coefficients.
Beckermann et al
| [7] | C. Beckermann, S. Ramadhyani and R. Viskanta, Natural convection flow and Heat Transfer between a fluid layer and a porous layer inside a rectangular enclosure, Journal of Heat Transfer, vol. 109, pp. 363-370, 1987. https://doi.org/10.1115/1.3248089 |
[7]
carried out a study in a closed cavity associated with a rectangular porous vessel. They were able to find agreement between numerical model results, temperature measurements and flow visualization. It can be seen that the amount of fluid flowing through the porous layer from the fluid region depends strongly on the Rayleigh (Ra) and Darcy (Da) numbers. Flow takes place mainly in the fluid layer and heat transfer into the porous layer takes place via the porous layer, if the relatively low product of Ra. Da.
Mbaye et al
| [8] | M. Mbaye, E. Bilgen and P. Vasseur, Natural-convection heat transfer in an inclined porous layer boarded by a finite-thickness wall, Int. Journal. Heat and Fluid Flow, vol. 14, pp. 244-291, 1993. https://doi.org/10.1016/0142-727X(93)90060-Z |
[8]
studied analytically and numerically the natural convection in a porous medium inclined by a wall of given thickness and thermal conductivity.
They gave their results in terms of the global Nusselt number as a function of Rayleigh and Darcy, the angle of inclination of the system, and the thickness and thermal conductivity of the wall.
Choukairy and Bennacer
| [9] | Choukairy, K., Bennacer, R. “Numerical and analytical analysis of the thermosolutal convection in an heterogeneous porous cavity”. FDMP-Fluid Dyn. Mater. Process. 8, 155- 172 (2012). https://doi.org/10.3970/fdmp.2012.008.155 |
[9]
carried out an analytical and numerical study of natural thermosolutal convection in heterogeneous porous media. The influence of Rayleigh number, inhomogeneity and buoyancy ratio on the Nusselt number (Nu) and Sherwood number (Sh) was analyzed.
Fajraoui et al
| [10] | Fajraoui, N., Fahs, M., Younes, A., Sudret, B. “Analyzing natural convection in porous enclosures with polynomial chaos expansions: effect of thermal dispersion, anisotropic permeability and heterogeneity”. Int. J. Heat Mass Transf. 115, 205-224 (2017). https://doi.org/10.1016/j.ijheatmasstransfer.2017.07.003 |
[10]
studied natural convection in a square porous cavity. They used a methodology that enables in-depth analyses to be carried out, providing information relevant to the interpretation of a natural convection problem in a porous medium at low computational cost.
Edimilson et al
studied turbulent natural convection in a square porous cavity using the macroscopic k-ԑ model. The results further indicate that when the parameters porosities, Pr, the conductivity ratio between fluid and solid matrix and Ra are held fixed, the lower the Darcy number, the higher the average Nusselt number at the hot wall.
Mobedi et al
showed the effect of conduction and Rayleigh number Ra in a numerical study of natural convection in a square enclosure. They deduce that increasing Ra and the ratio of thermal conductivities leads to an increase in natural convection. Heat transfer by natural convection in the cavity is reduced with increasing conductivity ratio when the Rayleigh number Ra = 106. For Ra = 103, the change in thermal conductivity λ has no effect on heat transfer by natural convection.
Other researchers have carried out studies on partitioned cavities without porous media.
Svoboda and Kubr
| [13] | Zbynek Svoboda and Marek Kubr (2011) Numerical simulation of heat transfer through hollow bricks in the vertical direction. Journal of Building Physics 34: 325-350. https://doi.org/10.1177/1744259113499214 |
[13]
used numerical simulation to study heat transfer through hollow bricks with vertical cavities. The results show that convective heat transfer in the cavity almost completely disappears when the cavity height is more than 20 times that of the cavity surface. In such cavities, radiation and conduction are the only modes of heat transfer.
Sambou et al
| [14] | Vincent Sambou, Berangere Lartigue, Francoise Monchoux and Mamadou Adj. Modeling of the thermal performance of air-filled partitioned enclosures: Effects of geometry and thermal properties. Journal of Building Physics; 2016, Vol. 39(4) 321-341. https://doi.org/10.1177/1744259114561578 |
[14]
theoretically and experimentally studied heat transfer through a partitioned cavity in order to determine and optimize thermal resistance. In another paper
| [15] | Vincent Sambou, Berangere Lartigue, Francoise Monchoux One-dimensional model of natural convection in differentially heated partitioned enclosures with conductive outer walls and vertical partitions. June 2009Journal of Thermal Science and Engineering Applications 1(2). https://doi.org/10.1115/1.3202795 |
[15]
, the same authors studied the effects of geometric and thermal parameters on the thermal performance of a partitioned cavity. The results show that radiative transfer inhibits convection.
The aim of this numerical study is to determine the influence of the presence of a porous medium in one of the cells on heat transfer in a partitioned cavity.
To do this, we developed a CFD model to determine the influence of the porous medium in the partitioned cavity, based on the results of streamlines, isotherms and Nusselt number. Next, the effect of the position of the porous medium was evaluated. Finally, we studied the influence of parameters such as wall conductivity, emissivity and Ra number variation on transfer.
2. Description of the Problem
The system under study (see
Figure 1) is a 2D partitioned cavity, with external length L = 317 mm and height H = 200 mm. Two external vertical walls surround the enclosure, with three equally spaced partitions. The outer walls are 8 mm thick, while the inner partitions have a finished thickness of e = 3 mm. Uniform temperatures, Th and Tc, are imposed on the vertical external surfaces of the walls. The cells are filled with air, while the horizontal external surfaces are adiabatic. The entire system is made from the same material. One of the cells is filled with a porous medium.
Figure 1. Geometry of the system.
Simplifying Assumptions and Mathematical Formulation Simplifying Assumptions
The following assumptions are made in this study:
1. the porous matrix is homogeneous isotropic and in thermodynamic equilibrium with the fluid (air).
2. the fluid is Newtonian;
3. the flow generated is stationary, laminar and two-dimensional;
4. the interaction between heat and mass transfer (Soret and Dufour effect) is negligible;
5. the thermophysical properties of the fluid are constant and determined from the reference temperature To;
6. In porous media, the extended Darcy equation is added, combining Brinkman and Forchheimer terms.
7. On the other hand, the density of the fluid in the volumetric forces term varies linearly with temperature T1 according to the Bousinesq approximation. This variation is given by the relationship:
8. air is a non-participating, transparent medium;
9. walls and partitions are considered gray bodies;
Mathematical Formulation
Based on the assumptions considered, the system of partial differential equations describing this problem is composed of the continuity equation, the momentum equations and the heat transfer equation.
It has introduced the following dimensionless variables:
u/u* = U; v/ u* = V; x/H = X; z/H = Z p =P (u*)2;
= (T-T0)/T (T=Tch– Tfr)
u* =/;=f(Cp)f; λ=/
The equations in a porous medium are then written in the following forms according to Nield and Bejan
.
the porous area:
Continuity:
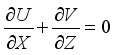 (1)
(1) Move:
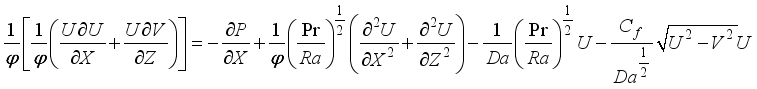 (2)
(2) 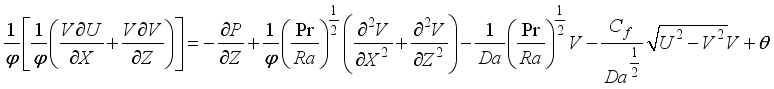 (3)
(3) Heat Thermal:
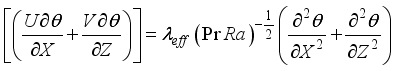 (4)
(4) The fluid area:
Continuity
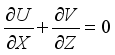 (5)
(5) Move
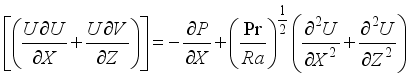 (6)
(6) 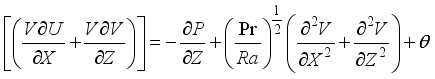 (7)
(7) Transfer of heat
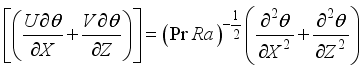 (8)
(8) Boundary condition
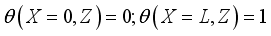 (9)
(9) Transfer radiative
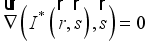 (10)
(10) 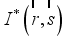
is the radiant intensity. It is given by the following relation:
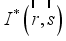
=
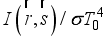 (11)
(11) The dimensionless equation for the radiative flux intensity at the boundary (X=X0) is given by the following relationship:
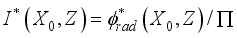 (12)
(12) In partitions and walls, the equation is:
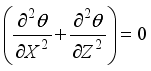 (13)
(13) At the vertical solid-fluid interface located at X = X0, temperatures verify:
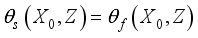 (14)
(14) The energy balance at point X = X0 (solid-fluid interface) can be deduced from this:
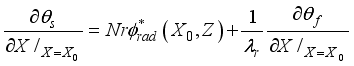 (15)
(15) The radiation and conduction interaction parameter Nr is given by the following relationship:
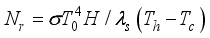 (16)
(16) The radiative flux density crossing the surface at points (X = X0, Z) is given by the following relationship:
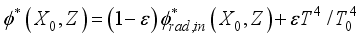 (17)
(17) 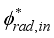
is called the flux density of incident radiation heat on the surface.
It is calculated by the following relationship:
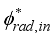
=
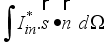 (18)
(18) Thermal transfer
It gives the rates transfers of heat convective and radiative on the walls and the partitions by the numbers of radiative and convective Nusselt are defined by:
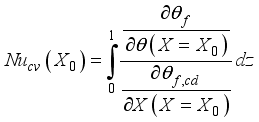 (19)
(19) 
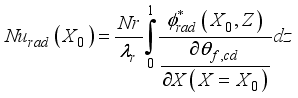 (20)
(20) θf, cd temperature of the fluid in the case or there is only conduction
3. Numerical Calculation
It uses the Ansys Fluent calculation code to solve the Navier-Stockes and heat equations. To do this, its used a uniform tetrahedral mesh. The test of independence of the solution with respect to mesh size is given in
Figure 2.
Figure 2. Flow versus number of elements.
4. Resultat and Validation of the Numerical Model
To validate our model, one uses the results of work by Sambou and al.
| [14] | Vincent Sambou, Berangere Lartigue, Francoise Monchoux and Mamadou Adj. Modeling of the thermal performance of air-filled partitioned enclosures: Effects of geometry and thermal properties. Journal of Building Physics; 2016, Vol. 39(4) 321-341. https://doi.org/10.1177/1744259114561578 |
| [15] | Vincent Sambou, Berangere Lartigue, Francoise Monchoux One-dimensional model of natural convection in differentially heated partitioned enclosures with conductive outer walls and vertical partitions. June 2009Journal of Thermal Science and Engineering Applications 1(2). https://doi.org/10.1115/1.3202795 |
[14, 15]
. Its considers a differentially heated square cavity. The Nusselt number results obtained are compared with those of Sambou and al.
| [14] | Vincent Sambou, Berangere Lartigue, Francoise Monchoux and Mamadou Adj. Modeling of the thermal performance of air-filled partitioned enclosures: Effects of geometry and thermal properties. Journal of Building Physics; 2016, Vol. 39(4) 321-341. https://doi.org/10.1177/1744259114561578 |
[14]
and Wang and al.
| [16] | Wang H, Xin S and Le Quere P (2006) Numerical study of the coupling of natural convection with surface radiation in an air-filled square cavity. Comptes Rendus Mécanique 334: 48-57. https://doi.org/10.1016/j.crme.2005.10.011 |
[16]
, which take account of convection-radiation coupling.
The results are shown in
Table 1.
Table 1. Comparison of Nusselt numbers for a square cavity (Ra = 106).
| | Wang et al. | [16] | Wang H, Xin S and Le Quere P (2006) Numerical study of the coupling of natural convection with surface radiation in an air-filled square cavity. Comptes Rendus Mécanique 334: 48-57. https://doi.org/10.1016/j.crme.2005.10.011 |
[16] | Sambou et al. | [15] | Vincent Sambou, Berangere Lartigue, Francoise Monchoux One-dimensional model of natural convection in differentially heated partitioned enclosures with conductive outer walls and vertical partitions. June 2009Journal of Thermal Science and Engineering Applications 1(2). https://doi.org/10.1115/1.3202795 |
[15] | Present study |
ԑ=0 | Nucv | 8.852 | 8.947 | 8.87 |
ԑ=0.2 | Nucv | 2.337 | 2.338 | 2.306 |
Nurad | 8.399 | 8.458 | 8.348 |
ԑ=0.8 | Nucv | 7.873 | 7.941 | 7.763 |
Nurad | 11.208 | 11.229 | 11.077 |
The
difference
between
our
results
and
those
of
| [15] | Vincent Sambou, Berangere Lartigue, Francoise Monchoux One-dimensional model of natural convection in differentially heated partitioned enclosures with conductive outer walls and vertical partitions. June 2009Journal of Thermal Science and Engineering Applications 1(2). https://doi.org/10.1115/1.3202795 |
[15]
and
| [16] | Wang H, Xin S and Le Quere P (2006) Numerical study of the coupling of natural convection with surface radiation in an air-filled square cavity. Comptes Rendus Mécanique 334: 48-57. https://doi.org/10.1016/j.crme.2005.10.011 |
[16]
does
not
exceed
2.22
.
5. Discussions
The cavity shown in
figure 1 is studied for numerical simulations. The cavity is made of PVC. The Rayleigh number is 1.9 10
7, and the emissivity is 0.9. The porous medium chosen is terracotta beads with porosity
= 0.55. Its aim is to examine the impact of the presence of a porous medium in a partitioned cavity cell, as well as the influence of certain physical parameters on heat transfer. For the analysis the results are presented in terms of streamlines, isotherms and Nusselt numbers.
1) Influence of the presence of porous media:
The streamlines and isotherms are shown in
figure 3 and
figure 4 respectively for (A) the partitioned cavity without porous medium and (B) with porous medium in the first cell. In
figure 3, we observe an absence of streamlines in the cavity containing the porous medium, indicating the absence of convection in this cavity. This is confirmed in
figure 4, where the isotherms of the first cell show a plateau in case (A) indicating established natural convection, while in case (B) the isotherms are parallel and quasi-vertical, proving a conductive heat transfer regime in the cell containing the porous medium. In the other cells, the shape of the isotherms (
Figure 4) remains virtually unchanged between cases (A) and (B), suggesting that the heat transfer mode remains the same. However, a slight variation in the flow lines indicates that the presence of the porous medium has an effect on heat transfer.
To quantify the impact of the presence of a porous medium,
Figure 5 shows the variation of the Nusselt number at point x = 84 mm as a function of height Y. The shape of the convective and radiative Nusselt number curves is the same whether or not the first cell contains a porous medium. The convective Nusselt number decreases overall as the Y dimension increases. This is due to the fact that Nusselt numbers are calculated on a hot face. At low and high Y values, the curves show peaks resulting from sudden temperature variations. Radiative Nusselt numbers increase with Y up to a certain height before decreasing. It can see that the convective and radiative Nusselt numbers in the case where the first cell contains a porous medium are lower than those in the case where the medium is absent. This suggests that the presence of a porous medium in the first cell reduces both convective and radiative heat transfer. The average convective Nusselt number falls from 4.5 to 4.0, while the average radiative Nusselt number drops from 10.8 to 8.2 with the introduction of the porous medium. It should be noted that radiative heat transfer is more significant than convective heat transfer.
Figure 3. Threads of currents.
Figure 5. Variation of the number of convective and radiative Nusselt.Variation of the number of convective and radiative Nusselt.
2) Influence of the position of the porous medium in the cells.
Figure 6 and
figure 7 show the streamlines and isotherms, respectively, in the case where the porous medium is in the first cell (A) or in the last cell (B). Analysis of the current lines (
figure 6) in the 2nd and 3rd cells in cases (A) and (B) shows a slight difference, suggesting that the position of the porous medium has very little influence on convective heat transfer in these cells. The same observations can be made by analyzing the isotherms (
figure 7).
Figure 6. Currents lines.
To quantify the influence of the porous medium's position on convective and radiative heat transfer,
Figure 8 shows the variation of the mean convective and radiative Nusselt numbers calculated at X=84 mm as a function of the porous medium's position.
The average convective and radiative Nusselt numbers decrease slightly when the porous medium is moved from the first cell to the last. The convective Nusselt number drops from 3.99 to 3.22, while the average radiative Nusselt number falls from 8.18 to 7.33 when the porous medium is moved from the first cell to the last cell. When the porous medium is close to the hot wall of the cell, its thermal gradient, noted Δθ, is low. As it moves away from this wall, Δθ increases, leading to an increase in conductive flux. This then induces a change in heat transfer.
Figure 8. Histogram of the convective and radiative numbers Nusselt.
Thus, it can conclude that the presence of the porous medium leads to a decrease in the rate of heat transfer, and that the position of the porous medium in the cells modifies this rate.
3) Influence of cell face thermal emissivity
Figure 9. Currents lines.
Keeping the same boundary conditions, i.e. a Rayleigh number of 1.9 10
7, It studies the configuration where the porous medium is in the first cell. It has varied the thermal emissivity of the partition faces and walls. To illustrate the impact of emissivity on heat transfer, it presents streamlines and isotherms for two cases (A) ԑ = 0.3 and (B) ԑ = 0.9. Current lines are shown in
Figure 9, while isotherms are illustrated in
figure 10. Significant differences are observed on the streamlines in both cases, suggesting that radiative transfer influences convective transfer. This is confirmed by the isotherms (
Figure 10), which show thermal stratification decreasing with increasing emissivity.
Figure 11. Variation of the mean Nusselt number (convective and radiative) as a function of emissivity ԑ.
Figure 11 shows the variation in average convective and radiative Nus-selt numbers calculated at X= 84 as a function of thermal emissivity.
The average convective Nusselt number decreases with increasing emissivity, from 5.4 to 3.3. This suggests that convective transfer is blocked by radiative transfer, homogenizing fluid-wall temperature along the y axis. As for the average radiative Nusselt number, it obviously increases almost linearly with emissivity, rising from 0 to 7.88.
4) Influence of the thermal conductivity of the cells
Maintaining the same boundary conditions (Ra = 1.9 x 10
7), he chooses the previous configuration and varies the thermal conductivity of the porous medium (0.3; 80).
Figures 12 and 13 show the current lines and isotherms respectively.
Figure 12 shows the behavior of the current lines in each partitioned cavity. It can be seen that the current lines are almost identical.
Figure 13 shows isotherms as a function of conductivity variation. It can be seen that thermal stratification decreases with increasing conductivity. This suggests that thermal conductivity has an influence on the thermal field.
Figure 14 shows the variation of the mean Nusselt number as a function of conductivity. The curve is divided into two parts (increasing and decreasing). The increasing part corresponds to the increase in conductivity, which leads to a decrease in the thermal gradient between the partitions. As a result, convective flow increases, which translates into higher Num in the cells.
The decreasing part of Num with increasing conductivity is due to the decreasing stratification of the thermal gradient, leading to an increase in the horizontal thermal gradient.
Figure 14 shows the same effects for the radiative Nusselt.
Figure 12. Currents lines.
Figure 14. Variation Num (convective; radiative) as a function of conductivity.
5) Influence of Rayleigh number on transfer
The correlation of the Nusselt number with the Rayleigh number is defined by the equation:
where W is a constant.
The graph in
figure 15 shows the variation of the average Nusselt number as a function of Ra. It note that the Nusselt number increases as Ra increases. This phenomenon can be explained by the increase in the intensity of the thrust forces, leading to an increase in the velocity of the convection currents and therefore in the intensity of the flow in the cells. An increase in Ra translates into an increase in heat transfer, so convective flow also increases, which explains the increase in Nuc as a function of Ra from 1.1 to 2.3.
As wall heat increases with Ra, radiative flux will also increase, resulting in an increase in the radiative Nusselt number from 4.3 to 17.2.
Figure 15. Variation Num (convective; radiative) as a function of Rayleigh number.
6. Conclusions
The aim of it studies was to determine the impact of the porous medium in a partitioned cavity by numerical simulation.
To this end, it developed a numerical model in Ansys Fluent to solve the Navier-Stokes and heat transfer equations. It then determined the Nusselt numbers as a function of the position of the porous medium and the effect of varying physical parameters.
In the first case, it observes that the presence of the porous medium reduces convection in this cavity. The further the porous medium is from the hot wall, the less heat transfer there is. The effect of radiative transfer reduces convection, and convective transfer decreases with increasing emissivity.
With regard to conductivity, It notes that Nusselt numbers (convective and radiative) increase as a function of λ up to a maximum value; after that, Nu begins to decrease as λ increases. Nusselt numbers (convective and radiative) increase with increasing Rayleigh number.
It plan to continue the work by varying the physical parameters of the porous medium, increasing the number of partitions in the cavity, and finally setting up an experimental setup.
Abbreviations
CFD: Dynamic Fluid Computer
DO: Discrete Ordinates
Conflicts of Interest
The authors declare no conflicts of interest.
References
| [1] |
Nield, D. A. and Bejan, A. (2006) Convection in Porous Media. Journal of Applied.
https://doi.org/10.4236/jamp.2022.1011218
|
| [2] |
T. Grosan, C. Revnic, I. Pop and D. Ingham, Magnetic field and internal heat generation.
https://doi.org/10.1016/j.ijheatmasstransfer.2008.08.011
|
| [3] |
F. Ouarhlent and A. Soudani Numerical study of the effect of permeability in a partially.
https://doi.org/10.18280/i2m.180303
|
| [4] |
J. Ordonez-Miranda, J. J. Alvarado-Gil Effect of pore shape on thermal conductivity of porous media) Journal of Materials Science volume 47, pages6733-6740 (2012).
https://doi.org/10.1007/s10853-012-6616-7
|
| [5] |
Belgacem Dhifaoui, Walid Foudhil, Sadok Ben Jabrallah, Ali Belghith. Study behavior of a porous medium traversed by an air flow and subjected to parietal heating. soumis `a chauffage parietal. Jean Jacques BEZIAN. JITH2007, Aug2007, Albis, France. hal-00161178, version 1 (29-08-2007).
|
| [6] |
M. K. Alkam, M. A. Al-Nimr, M. O. Hamdan “Enhancing heat transfer in parallel-plate channels by using porous inserts” Journal of Heat and Mass Transfer 44 (2001) 931-938.
https://doi.org/10.1016/S0017-9310(00)00155-1
|
| [7] |
C. Beckermann, S. Ramadhyani and R. Viskanta, Natural convection flow and Heat Transfer between a fluid layer and a porous layer inside a rectangular enclosure, Journal of Heat Transfer, vol. 109, pp. 363-370, 1987.
https://doi.org/10.1115/1.3248089
|
| [8] |
M. Mbaye, E. Bilgen and P. Vasseur, Natural-convection heat transfer in an inclined porous layer boarded by a finite-thickness wall, Int. Journal. Heat and Fluid Flow, vol. 14, pp. 244-291, 1993.
https://doi.org/10.1016/0142-727X(93)90060-Z
|
| [9] |
Choukairy, K., Bennacer, R. “Numerical and analytical analysis of the thermosolutal convection in an heterogeneous porous cavity”. FDMP-Fluid Dyn. Mater. Process. 8, 155- 172 (2012).
https://doi.org/10.3970/fdmp.2012.008.155
|
| [10] |
Fajraoui, N., Fahs, M., Younes, A., Sudret, B. “Analyzing natural convection in porous enclosures with polynomial chaos expansions: effect of thermal dispersion, anisotropic permeability and heterogeneity”. Int. J. Heat Mass Transf. 115, 205-224 (2017).
https://doi.org/10.1016/j.ijheatmasstransfer.2017.07.003
|
| [11] |
J. B. Edimilson and J. S., Marcelo de Lemos, Turbulent natural convection in a porous square cavity computed with a macroscopic K- ε model, International Journal of Heat and Mass Transfer, Vol. 47, pp. 5639-5650, 2004.
https://doi.org/10.1016/j.ijheatmasstransfer.2004.07.017
|
| [12] |
M. Mobedi, Conjugate natural convection in a square cavity with finite thickness horizontal walls, Int. Communication in Heat and Mass Transfer, vol. 35, pp. 503-513, 2008.
https://doi.org/10.1016/j.iheatmasstransfer.2007.09.004
|
| [13] |
Zbynek Svoboda and Marek Kubr (2011) Numerical simulation of heat transfer through hollow bricks in the vertical direction. Journal of Building Physics 34: 325-350.
https://doi.org/10.1177/1744259113499214
|
| [14] |
Vincent Sambou, Berangere Lartigue, Francoise Monchoux and Mamadou Adj. Modeling of the thermal performance of air-filled partitioned enclosures: Effects of geometry and thermal properties. Journal of Building Physics; 2016, Vol. 39(4) 321-341.
https://doi.org/10.1177/1744259114561578
|
| [15] |
Vincent Sambou, Berangere Lartigue, Francoise Monchoux One-dimensional model of natural convection in differentially heated partitioned enclosures with conductive outer walls and vertical partitions. June 2009Journal of Thermal Science and Engineering Applications 1(2).
https://doi.org/10.1115/1.3202795
|
| [16] |
Wang H, Xin S and Le Quere P (2006) Numerical study of the coupling of natural convection with surface radiation in an air-filled square cavity. Comptes Rendus Mécanique 334: 48-57.
https://doi.org/10.1016/j.crme.2005.10.011
|
Cite This Article
-
ACS Style
Faye, S.; Diarra, S.; Sokhna, S. M.; Sambou, V. Numerical Study of Heat Transfer in a Partitioned Cavity Containing a Porous Medium. Appl. Eng. 2024, 8(1), 31-40. doi: 10.11648/j.ae.20240801.13
 Copy
|
Copy
|
 Download
Download
-
@article{10.11648/j.ae.20240801.13,
author = {Souleye Faye and Sory Diarra and Sidy Mactar Sokhna and Vincent Sambou},
title = {Numerical Study of Heat Transfer in a Partitioned Cavity Containing a Porous Medium
},
journal = {Applied Engineering},
volume = {8},
number = {1},
pages = {31-40},
doi = {10.11648/j.ae.20240801.13},
url = {https://doi.org/10.11648/j.ae.20240801.13},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ae.20240801.13},
abstract = {Cavities separated by multiple vertical partitions and filled with a porous medium present a remarkable thermal insulation quality, offering potential solutions in various engineering fields. The aim of this study is to analyze the impact of the presence of a porous medium on heat transfer through a partitioned cavity. We have developed a numerical model based on the Navier-Stokes and heat transfer equations, solved using Ansys Fluent software. We examine the evolution of the Nusselt number (convection and radiation) as a function of the position of the porous medium inside the cavity, as well as physical properties such as emissivity, wall conductivity and Rayleigh number. Current lines and isotherms are obtained from this numerical model. Nusselt numbers for both convection and radiation are calculated, taking into account the position of the porous medium in the system, as well as the effect of varying physical parameters on heat transfer. It has been observed that the presence of the porous medium leads to a reduction in the rate of heat transfer within the cavity. The further the porous medium is from the hot wall, the more pronounced this reduction. In addition, radiative transfer has a downward influence on convective transfer. Furthermore, the convective transfer rate decreases with increasing emissivity. As far as conductivity is concerned, transfer rates (convective and radiative) initially increase until a maximum Nusselt number is reached, after which they gradually decrease with a further increase in conductivity. Nusselt numbers (convection and radiation) increase as the Rayleigh number increases.
},
year = {2024}
}
 Copy
|
Copy
|
 Download
Download
-
TY - JOUR
T1 - Numerical Study of Heat Transfer in a Partitioned Cavity Containing a Porous Medium
AU - Souleye Faye
AU - Sory Diarra
AU - Sidy Mactar Sokhna
AU - Vincent Sambou
Y1 - 2024/04/17
PY - 2024
N1 - https://doi.org/10.11648/j.ae.20240801.13
DO - 10.11648/j.ae.20240801.13
T2 - Applied Engineering
JF - Applied Engineering
JO - Applied Engineering
SP - 31
EP - 40
PB - Science Publishing Group
SN - 2994-7456
UR - https://doi.org/10.11648/j.ae.20240801.13
AB - Cavities separated by multiple vertical partitions and filled with a porous medium present a remarkable thermal insulation quality, offering potential solutions in various engineering fields. The aim of this study is to analyze the impact of the presence of a porous medium on heat transfer through a partitioned cavity. We have developed a numerical model based on the Navier-Stokes and heat transfer equations, solved using Ansys Fluent software. We examine the evolution of the Nusselt number (convection and radiation) as a function of the position of the porous medium inside the cavity, as well as physical properties such as emissivity, wall conductivity and Rayleigh number. Current lines and isotherms are obtained from this numerical model. Nusselt numbers for both convection and radiation are calculated, taking into account the position of the porous medium in the system, as well as the effect of varying physical parameters on heat transfer. It has been observed that the presence of the porous medium leads to a reduction in the rate of heat transfer within the cavity. The further the porous medium is from the hot wall, the more pronounced this reduction. In addition, radiative transfer has a downward influence on convective transfer. Furthermore, the convective transfer rate decreases with increasing emissivity. As far as conductivity is concerned, transfer rates (convective and radiative) initially increase until a maximum Nusselt number is reached, after which they gradually decrease with a further increase in conductivity. Nusselt numbers (convection and radiation) increase as the Rayleigh number increases.
VL - 8
IS - 1
ER -
 Copy
|
Copy
|
 Download
Download
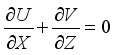 (1)
(1) 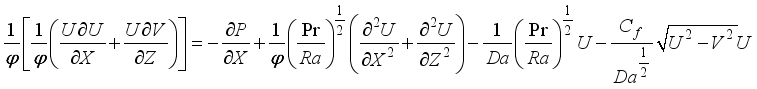 (2)
(2) 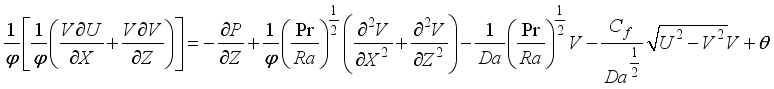 (3)
(3) 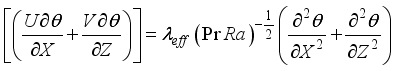 (4)
(4) 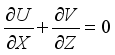 (5)
(5) 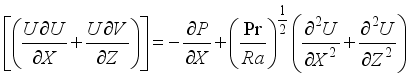 (6)
(6) 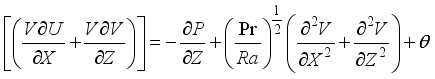 (7)
(7) 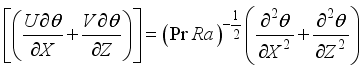 (8)
(8) 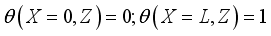 (9)
(9) 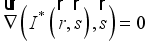 (10)
(10) 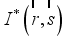 is the radiant intensity. It is given by the following relation:
is the radiant intensity. It is given by the following relation: 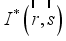 =
= 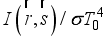 (11)
(11) 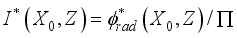 (12)
(12) 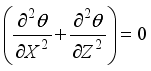 (13)
(13) 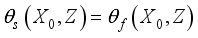 (14)
(14) 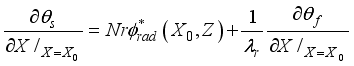 (15)
(15) 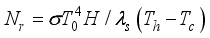 (16)
(16) 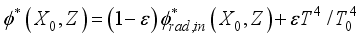 (17)
(17) 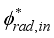 is called the flux density of incident radiation heat on the surface.
is called the flux density of incident radiation heat on the surface. 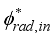 =
= 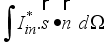 (18)
(18) 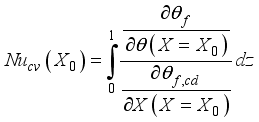 (19)
(19) 
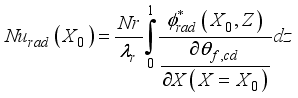 (20)
(20)